System Dynamics of a Bank Run

Bank runs are psychological phenomena feeding off inherent vulnerabilities in bank structure and function. These vulnerabilities have been covered thoroughly in the past few weeks, prompting ideas for how the banking system might be restructured to increase resilience. 

For now, just as pandemics end socially, so do bank runs. In 2009, conducting and publicly reporting results of capital stress tests was reassuring enough that the financial sector began to recover. In this round of financial stress, the solution may look similar or different, but it will (either deliberately or by accident) succeed by influencing a leverage point.

In system dynamics, leverage points are “places within a complex system … where a small shift in one thing can produce big changes in everything,” as Donella Meadows, author of Thinking in Systems, puts it. They are sometimes but not always intuitive.

Causal loop diagrams, especially when coupled with simulation modeling, can help identify leverage points. (They also can help identify actions that seem like they should help but don’t actually move the needle much—and this can save a ton of wasted time and effort!)

Causal loops for bank runs

Let’s walk through some causal loop diagrams for bank runs. Briefly, causal loop diagrams follow cause and effect to try to determine:

• How a system will behave under different conditions.

• How to shift the system toward beneficial outcomes.

For a more complete introduction to causal loop diagrams, my primer on drawing causal loops walks through them in detail.

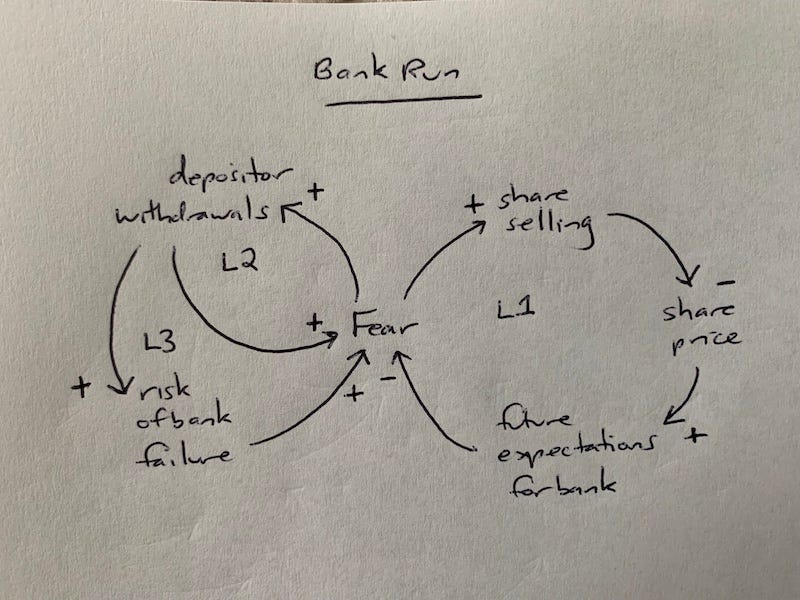
Here’s a high-level diagram of how a bank run might function for a small traditional bank that is publicly traded (I’ve abstracted away a lot of detail to highlight the leverage point): 

Breaking down the causal loop into manageable pieces

This diagram looks somewhat simple, but it can still be a bit complex to read it. Here’s how: to read the diagram, first assess each pair of components in isolation. We’ll put it all together later.

Here’s how each pair of isolated components looks (by convention, we always start these statements with the first component increasing):

• If future expectations for the bank go up (increase), then fear goes down (an inverse relationship; in plain English, they move in opposite directions).

• If fear goes up, share selling goes up (a direct relationship; in plain English, they move in the same direction).

• If share selling goes up, share price goes down (an inverse relationship).

• If share price goes up, future expectations for the bank go up (a direct relationship).

• If fear goes up, depositor withdrawals go up (a direct relationship).

• If depositor withdrawals go up, fear goes up (a direct relationship).

• If depositor withdrawals go up, risk of bank failure goes up (a direct relationship).

• If risk of bank failure goes up, fear goes up (a direct relationship).

Getting the big picture

Now we’ll put it all together. There are three loops in this diagram, labeled L1, L2, and L3.

• L1: If fear goes up, share selling goes up, which will cause the share price to go down, which will cause future expectations for the bank to decrease, which will cause fear to increase, which will cause share selling to increase, which will cause the share price to go down, and so on. That’s a reinforcing loop. (Shortcut: On the diagram, you can see there’s a zero or even number of negative signs: two, in this case. That means a reinforcing loop!)

• L2: If fear goes up, depositor withdrawals increase, which will cause fear to increase, and so on. Another reinforcing loop! (Shortcut: This one has zero negative signs. That’s reinforcing.)

• L3: If fear goes up, depositor withdrawals increase, which will increase the risk of bank failure (for various reasons that are abstracted out of this diagram), which will cause fear to increase, and so on. Yep, it’s also a reinforcing loop.

The interaction among these loops is quite vicious¹ and encapsulates, at a high level, the basic vulnerability of banking business models: no bank can survive a sufficiently intense and accelerating run without action that halts the mechanisms of the loop. And if you look at the diagram, it pretty clearly shows what we know: the only thing that ends a bank run is a decrease in fear, which stops the cycle. Fear is the leverage point where all loops converge. Matt Levine had a great post on how banking is a confidence game.

Zeroing in on fear

So, if fear is the leverage point, then if we can change the level of fear in the system, we can reverse the direction of all these loops. Let’s look at what happens if fear goes down, not up (perhaps because of capital stress tests as in 2009, or because of depositor guarantees from the FDIC, or because a coalition of large banks makes deposits at a smaller bank). If those efforts work, what happens in our diagram? Follow the flows: 

• If fear goes down, share selling goes down, which will cause share price to go up, which will cause future expectations for the bank to go up, which will further reduce fear, and so on. (It’s still a reinforcing loop, but now it’s working for us.) 

• Also and simultaneously, if fear goes down, depositor withdrawals decrease, which will reduce fear and reduce the risk of bank failure, which will further reduce fear.  

Suddenly those scary loops are working in our favor, as long as fear continues to decrease.

This is the power of leverage points. Even if we take some of that abstraction away and show more detail, does the leverage point change? No, fear is still a leverage point, although another possible leverage point also becomes visible. Can you see what it is?

Modeling to find subtle leverage points

That brings up another point. Not all leverage points are obvious. Some leverage points can be quite subtle, especially in large and complex systems. That’s where modeling can play a key role, allowing you to run thousands of simulations to identify which changes produce the greatest beneficial effects. 

Some system dynamics modeling tools include (I’m not affiliated with any of these) Vensim, Powersim Studio, and iThink/STELLA. The System Dynamics Society has a rundown of these and other tools and extensions.

The sweet spot for system dynamics

To wrap up, let’s talk about optimal uses for system dynamics modeling. Historically, it’s been particularly useful for long-term planning and improvement, not just because model creation and validation historically has been time-intensive², but also because changes arising from action on a leverage point can take a while to work their way through a system. Changes can only propagate at the speed of the overall system, so they are subject to bottlenecks and delays like any other part of the system. While changes are propagating through a system, they may be vulnerable to organizational pressures until their effect materializes.

Some areas where system dynamics modeling can play an important role include (among many others):

• Climate change mitigation.

• Increasing organizational or systemic efficiency and effectiveness.

• Choosing among multiple policy options to increase wellbeing of a population.

The history of system dynamics is one of success in predicting trajectories, as Gaya Herrington confirmed in her 2020 assessment of the 1972 and 2002 Limits to Growth predictions, and in achieving or exceeding target outcomes where it has been rigorously implemented and supported by stakeholders, as documented in numerous System Dynamics Society case studies.

That sounds like a mouthful, but in essence: it works if stakeholders buy in and make the changes that well-crafted, well-supported models suggest.

1. Yes, I do think that being publicly traded might increase the likelihood of a bank run, simply because there are probably more eyes on the bank’s financial statements (both long investors and short-sellers) and therefore more people who might potentially tweet or call out hypothesized or actual weaknesses. Bank runs are often psychologically driven.

2. Technology advances may speed up the process of gathering accurate data from multiple disparate systems and compiling that data into effective system dynamics models.